Kako pronaći područje baze pravilne piramide. Površina četverokutne piramide

Površina piramide. U ovom ćemo članku razmotriti probleme s pravilnim piramidama. Dopustite mi da vas podsjetim da je pravilna piramida piramida čija je baza pravilan mnogokut, vrh piramide je projiciran u središte tog mnogokuta.

Bočna strana takve piramide je jednakokračni trokut.Visina ovog trokuta izvučena iz vrha pravilne piramide naziva se apotem, SF - apotem:

U dolje prikazanoj vrsti problema morate pronaći površinu cijele piramide ili površinu njezine bočne površine. Blog je već raspravljao o nekoliko problema s pravilnim piramidama, gdje je pitanje bilo o pronalaženju elemenata (visina, osnovni rub, bočni rub).

Zadaci Jedinstvenog državnog ispita obično ispituju pravilne trokutaste, četverokutne i šesterokutne piramide. Nisam vidio nikakvih problema s pravilnim peterokutnim i sedmerokutnim piramidama.

Formula za površinu cijele površine je jednostavna - trebate pronaći zbroj površine baze piramide i površine njezine bočne površine:

Razmotrimo zadatke:

Stranice baze pravilne četverokutne piramide su 72, bočni bridovi su 164. Nađite površinu ove piramide.

Površina piramide jednaka je zbroju površina bočne površine i baze:

*Bočnu plohu čine četiri trokuta jednake površine. Osnova piramide je kvadrat.

Možemo izračunati površinu strane piramide koristeći:

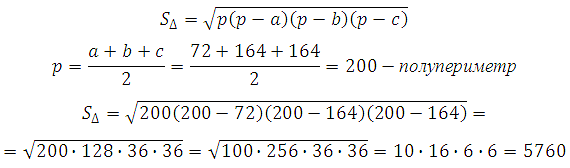
Dakle, površina piramide je:

Odgovor: 28224

Stranice baze pravilne šesterokutne piramide jednake su 22, bočni rubovi su jednaki 61. Nađite bočnu površinu ove piramide.

Osnova pravilne šesterokutne piramide je pravilni šesterokut.

Bočna površina ove piramide sastoji se od šest područja jednakih trokuta sa stranicama 61,61 i 22:

Nađimo površinu trokuta pomoću Heronove formule:

Dakle, bočna površina je:

Odgovor: 3240

*U gore navedenim problemima, područje bočne strane može se pronaći pomoću druge formule trokuta, ali za to morate izračunati apotemu.

27155. Odredite površinu pravilne četverokutne piramide čije su osnovne stranice 6, a visina 4.

Da bismo pronašli površinu piramide, moramo znati površinu baze i površinu bočne površine:

Površina baze je 36 jer je to kvadrat sa stranicom 6.

Bočna površina sastoji se od četiri lica, koja su jednaki trokuti. Da biste pronašli područje takvog trokuta, morate znati njegovu bazu i visinu (apotem):

*Površina trokuta jednaka je polovici umnoška baze i visine povučene na tu bazu.

Baza je poznata, jednaka je šest. Nađimo visinu. Razmotrimo pravokutni trokut (označen žutom bojom):

Jedan krak je jednak 4, jer je to visina piramide, drugi je jednak 3, jer je jednak polovici ruba baze. Hipotenuzu možemo pronaći pomoću Pitagorine teoreme:

To znači da je površina bočne površine piramide:

Dakle, površina cijele piramide je:

Odgovor: 96

27069. Stranice baze pravilne četverokutne piramide jednake su 10, bočni bridovi su jednaki 13. Nađite površinu ove piramide.

27070. Stranice baze pravilne šesterokutne piramide jednake su 10, bočni bridovi su jednaki 13. Nađite bočnu površinu ove piramide.

Postoje i formule za bočnu površinu pravilne piramide. U pravilnoj piramidi baza je ortogonalna projekcija bočne plohe, dakle:

P- osnovni opseg, l- apotem piramide

*Ova formula se temelji na formuli za površinu trokuta.

Ako želite saznati više o tome kako se te formule izvode, ne propustite, pratite objavljivanje članaka.To je sve. Sretno ti!

S poštovanjem, Alexander Krutitskikh.

P.S: Bio bih vam zahvalan ako biste mi rekli nešto o stranici na društvenim mrežama.

Prije proučavanja pitanja o ovoj geometrijskoj figuri i njenim svojstvima, trebali biste razumjeti neke pojmove. Kad čovjek čuje za piramidu, zamišlja ogromne građevine u Egiptu. Ovako izgledaju oni najjednostavniji. Ali dolaze u različitim vrstama i oblicima, što znači da će formula za izračun geometrijskih oblika biti drugačija.

Piramida - geometrijski lik, označavajući i predstavljajući nekoliko lica. U biti, ovo je isti poliedar, u čijoj osnovi leži poligon, a na stranama su trokuti koji se spajaju u jednoj točki - vrhu. Figura dolazi u dvije glavne vrste:

• ispravan;
• krnji.

U prvom slučaju baza je pravilan poligon. Ovdje su sve bočne površine jednake između sebe i same figure ugodit će oku perfekcionista.

U drugom slučaju postoje dvije baze - velika na samom dnu i mala između vrha, ponavljajući oblik glavne. Drugim riječima, krnja piramida je poliedar s presjekom formiranim paralelno s bazom.

Termini i simboli

Ključni pojmovi:

• Pravilni (jednakostranični) trokut- lik s tri jednaka kuta i jednakim stranicama. U ovom slučaju svi kutovi su 60 stupnjeva. Figura je najjednostavniji pravilni poliedar. Ako ta figura leži na bazi, tada će se takav poliedar nazvati pravilnim trokutastim. Ako je baza kvadrat, piramida će se zvati pravilna četverokutna piramida.
• Vertex– najviša točka gdje se spajaju rubovi. Visinu vrha oblikuje ravna linija koja se proteže od vrha do baze piramide.
• Rub– jedna od ravnina poligona. Može biti u obliku trokuta u slučaju trokutaste piramide ili u obliku trapeza kod krnje piramide.
• Odjeljak- ravna figura nastala kao rezultat disekcije. Ne treba ga brkati s odjeljkom, budući da odjeljak također pokazuje što se nalazi iza odjeljka.
• Apotema- segment nacrtan od vrha piramide do njezine baze. To je ujedno i visina lica na kojoj se nalazi druga visinska točka. Ova definicija vrijedi samo u odnosu na pravilan poliedar. Na primjer, ako ovo nije krnja piramida, tada će lice biti trokut. U ovom slučaju, visina ovog trokuta postat će apotem.

Formule za površine

Nađite površinu bočne površine piramide bilo koja vrsta može se izvesti na nekoliko načina. Ako lik nije simetričan i poligon je s različitim stranama, tada je u tom slučaju lakše izračunati ukupnu površinu kroz ukupnost svih površina. Drugim riječima, trebate izračunati površinu svakog lica i zbrojiti ih.

Ovisno o tome koji su parametri poznati, mogu biti potrebne formule za izračun kvadrata, trapeza, proizvoljnog četverokuta itd. Same formule u različitim slučajevima također će imati razlike.

U slučaju pravilne figure, pronalaženje područja je puno lakše. Dovoljno je znati samo nekoliko ključnih parametara. U većini slučajeva izračuni su potrebni posebno za takve brojke. Stoga će u nastavku biti dane odgovarajuće formule. Inače biste morali sve ispisivati ​​na nekoliko stranica, što bi vas samo zbunjivalo i zbunjivalo.

Osnovna formula za izračun Bočna površina pravilne piramide imat će sljedeći oblik:

S=½ Pa (P je opseg baze i apotem)

Pogledajmo jedan primjer. Poliedar ima bazu sa segmentima A1, A2, A3, A4, A5, a svi su jednaki 10 cm. Neka je apotem jednak 5 cm. Prvo treba pronaći opseg. Budući da je svih pet lica baze isto, možete ga pronaći ovako: P = 5 * 10 = 50 cm Zatim primjenjujemo osnovnu formulu: S = ½ * 50 * 5 = 125 cm na kvadrat.

Bočna površina pravilne trokutaste piramide najlakše izračunati. Formula izgleda ovako:

S =½* ab *3, gdje je a apotem, b lice baze. Faktor tri ovdje znači broj lica baze, a prvi dio je površina bočne površine. Pogledajmo primjer. Zadan je lik s apotemom 5 cm i osnovnim rubom 8 cm. Računamo: S = 1/2*5*8*3=60 cm na kvadrat.

Bočna površina krnje piramide Malo je teže izračunati. Formula izgleda ovako: S =1/2*(p_01+ p_02)*a, gdje su p_01 i p_02 perimetri baza, a apotem. Pogledajmo primjer. Recimo da su za četverokutni lik dimenzije stranica baza 3 i 6 cm, a apotema 4 cm.

Ovdje prvo morate pronaći opsege baza: r_01 =3*4=12 cm; r_02=6*4=24 cm Ostaje zamijeniti vrijednosti u glavnu formulu i dobivamo: S =1/2*(12+24)*4=0,5*36*4=72 cm na kvadrat.

Tako možete pronaći bočnu površinu pravilne piramide bilo koje složenosti. Treba biti oprezan i ne zbuniti se ove izračune s ukupnom površinom cijelog poliedra. A ako to još trebate učiniti, samo izračunajte površinu najveće baze poliedra i dodajte je površini bočne površine poliedra.

Video

Ovaj video će vam pomoći da konsolidirate informacije o tome kako pronaći bočnu površinu različitih piramida.

Niste dobili odgovor na svoje pitanje? Predložite temu autorima.

Tipični geometrijski problemi na ravnini iu trodimenzionalnom prostoru su problemi određivanja površina različitih likova. U ovom članku predstavljamo formulu za bočnu površinu pravilne četverokutne piramide.

Što je piramida?

Dajmo strogu geometrijsku definiciju piramide. Pretpostavimo da imamo mnogokut s n stranica i n kutova. Izaberimo proizvoljnu točku u prostoru koja neće biti u ravnini navedenog n-kuta i spojimo je sa svakim vrhom poligona. Dobit ćemo lik određenog volumena, koji se naziva n-kutna piramida. Na primjer, pokažimo na donjoj slici kako izgleda peterokutna piramida.

Dva važna elementa svake piramide su njena baza (n-kut) i njen vrh. Ti su elementi međusobno povezani s n trokuta koji općenito nisu međusobno jednaki. Okomica koja se s vrha spušta na bazu naziva se visina lika. Ako siječe bazu u geometrijskom središtu (poklapa se sa središtem mase mnogokuta), tada se takva piramida naziva ravnom crtom. Ako je uz ovaj uvjet baza pravilan mnogokut, tada se cijela piramida naziva pravilnom. Slika ispod pokazuje kako izgledaju pravilne piramide s trokutastim, četverokutnim, peterokutnim i šesterokutnim bazama.

Površina piramide

Prije nego što prijeđemo na pitanje bočne površine pravilne četverokutne piramide, trebali bismo se detaljnije zadržati na konceptu same površine.

Kao što je gore spomenuto i prikazano na slikama, svaku piramidu čini skup lica ili stranica. Jedna stranica je baza, a n stranica su trokuti. Površina cijelog lika je zbroj površina svake njegove stranice.

Prikladno je proučavati površinu pomoću primjera razvoja figure. Razvoj pravilne četverokutne piramide prikazan je na slikama ispod.

Vidimo da je njegova površina jednaka zbroju četiri površine identičnih jednakokračnih trokuta i površine kvadrata.

Ukupna površina svih trokuta koji tvore stranice figure obično se naziva bočna površina. Zatim ćemo pokazati kako to izračunati za pravilnu četverokutnu piramidu.

Bočna površina četverokutne pravilne piramide

Da bismo izračunali bočnu površinu navedene figure, ponovno se okrećemo gore navedenom razvoju. Pretpostavimo da znamo stranicu kvadratne baze. Označimo ga simbolom a. Vidi se da svaki od četiri jednaka trokuta ima osnovicu duljine a. Da biste izračunali njihovu ukupnu površinu, morate znati ovu vrijednost za jedan trokut. Iz tečaja geometrije znamo da je površina S t trokuta jednaka umnošku osnovice i visine koju treba podijeliti na pola. To je:

Gdje je h b visina jednakokračnog trokuta povučena na osnovicu a. Za piramidu, ova visina je apotem. Sada preostaje pomnožiti dobiveni izraz s 4 da bi se dobila površina S b bočne plohe dotične piramide:

S b = 4*S t = 2*h b *a.

Ova formula sadrži dva parametra: apotemu i stranicu baze. Ako je potonji poznat u većini uvjeta problema, tada se prvi mora izračunati uz poznavanje drugih veličina. Ovdje su formule za izračunavanje apoteme h b za dva slučaja:

• kada je poznata duljina bočnog rebra;
• kada je poznata visina piramide.

Ako duljinu bočnog brida (stranice jednakokračnog trokuta) označimo simbolom L, tada se apotem h b određuje formulom:

h b = √(L 2 - a 2 /4).

Ovaj izraz je rezultat primjene Pitagorinog poučka na trokut bočne površine.

Ako je poznata visina h piramide, tada se apotem h b može izračunati na sljedeći način:

h b = √(h 2 + a 2 /4).

Također nije teško dobiti ovaj izraz ako uzmemo u obzir pravokutni trokut unutar piramide kojeg čine katete h i a/2 i hipotenuza h b.

Pokažimo kako primijeniti ove formule rješavajući dva zanimljiva problema.

Problem s poznatom površinom

Poznato je da je površina bočne površine četverokuta 108 cm 2. Potrebno je izračunati duljinu njezina apotema h b ako je visina piramide 7 cm.

Napišimo formulu za površinu S b bočne plohe u smislu visine. Imamo:

S b = 2*√(h 2 + a 2 /4) *a.

Ovdje smo jednostavno zamijenili odgovarajuću formulu apoteme u izraz za S b. Kvadriramo obje strane jednadžbe:

S b 2 = 4*a 2 *h 2 + a 4.

Da bismo pronašli vrijednost a, mijenjamo varijable:

t 2 + 4*h 2 *t - S b 2 = 0.

Sada zamijenimo poznate vrijednosti i riješimo kvadratnu jednadžbu:

t 2 + 196*t - 11664 = 0.

Zapisali smo samo pozitivni korijen ove jednadžbe. Tada će stranice baze piramide biti jednake:

a = √t = √47,8355 ≈ 6,916 cm.

Da biste dobili duljinu apoteme, samo upotrijebite formulu:

h b = √(h 2 + a 2 /4) = √(7 2 + 6,916 2 /4) ≈ 7,808 cm.

Bočna površina Keopsove piramide

Odredimo vrijednost bočne površine za najveću egipatsku piramidu. Poznato je da u njegovoj osnovi leži kvadrat sa stranicom duljine 230,363 metra. Visina strukture izvorno je bila 146,5 metara. Zamijenimo ove brojeve u odgovarajuću formulu za S b, dobivamo:

S b = 2*√(h 2 + a 2 /4) *a = 2*√(146,5 2 +230,363 2 /4)*230,363 ≈ 85860 m 2.

Pronađena vrijednost nešto je veća od površine 17 nogometnih igrališta.

Definicija. Bočni rub- ovo je trokut u kojem jedan kut leži na vrhu piramide, a suprotna strana se podudara sa stranom baze (poligon).

Definicija. Bočna rebra- ovo su uobičajene strane bočnih strana. Piramida ima onoliko bridova koliko kutova ima mnogokut.

Definicija. Visina piramide- ovo je okomica spuštena od vrha do baze piramide.

Definicija. Apotema- ovo je okomica na bočnu stranu piramide, spuštena s vrha piramide na stranu baze.

Definicija. Dijagonalni presjek- ovo je presjek piramide ravninom koja prolazi kroz vrh piramide i dijagonalu baze.

Definicija. Ispravna piramida je piramida kojoj je baza pravilan mnogokut, a visina se spušta do središta baze.

Volumen i površina piramide

Formula. Volumen piramide kroz osnovnu površinu i visinu:

Svojstva piramide

Ako su svi bočni rubovi jednaki, tada se oko baze piramide može nacrtati krug, a središte baze se poklapa sa središtem kruga. Također, okomica spuštena s vrha prolazi središtem baze (kružnice).

Ako su svi bočni rubovi jednaki, tada su nagnuti prema ravnini baze pod istim kutovima.

Bočni bridovi su jednaki kada tvore jednake kutove s ravninom baze ili ako se oko baze piramide može opisati kružnica.

Ako su bočne strane nagnute prema ravnini baze pod istim kutom, tada se krug može upisati u bazu piramide, a vrh piramide projicira se u njenom središtu.

Ako su bočne plohe nagnute prema ravnini baze pod istim kutom, onda su apoteme bočnih ploha jednake.

Svojstva pravilne piramide

1. Vrh piramide je jednako udaljen od svih kutova baze.

2. Svi bočni rubovi su jednaki.

3. Sva bočna rebra su nagnuta pod jednakim kutom u odnosu na bazu.

4. Apoteme svih bočnih lica su jednake.

5. Površine svih bočnih ploha su jednake.

6. Sve plohe imaju iste diedralne (ravne) kutove.

7. Oko piramide se može opisati kugla. Središte opisane sfere bit će sjecište okomica koje prolaze kroz sredinu bridova.

8. Kuglu možete uklopiti u piramidu. Središte upisane sfere bit će točka presjeka simetrala koje izlaze iz kuta između brida i baze.

9. Ako se središte upisane sfere poklapa sa središtem opisane sfere, tada je zbroj ravninskih kutova pri vrhu jednak π ili obrnuto, jedan kut je jednak π/n, gdje je n broj kutova na dnu piramide.

Veza piramide i kugle

Oko piramide se može opisati sfera kada se u osnovi piramide nalazi poliedar oko kojeg se može opisati kružnica (nužan i dovoljan uvjet). Središte sfere bit će sjecište ravnina koje prolaze okomito kroz središta bočnih bridova piramide.

Uvijek je moguće opisati sferu oko bilo koje trokutaste ili pravilne piramide.

U piramidu se može upisati kugla ako se simetrale unutarnjih diedarskih kutova piramide sijeku u jednoj točki (nužan i dovoljan uvjet). Ova točka će biti središte sfere.

Veza piramide sa stošcem

Kaže se da je stožac upisan u piramidu ako se njihovi vrhovi poklapaju, a baza stošca je upisana u bazu piramide.

Stožac se može upisati u piramidu ako su apoteme piramide međusobno jednake.

Kaže se da je stožac opisan oko piramide ako se njihovi vrhovi poklapaju, a baza stošca je opisana oko baze piramide.

Stožac se može opisati oko piramide ako su svi bočni bridovi piramide međusobno jednaki.

Odnos piramide i valjka

Piramida se naziva upisana u valjak ako vrh piramide leži na jednoj osnovici valjka, a baza piramide je upisana u drugu bazu cilindra.

Oko piramide se može opisati cilindar ako se oko baze piramide može opisati kružnica.

Definicija. Krnja piramida (piramidalna prizma) je poliedar koji se nalazi između baze piramide i presječne ravnine paralelne s bazom. Tako piramida ima veću bazu i manju bazu koja je slična većoj. Bočna lica su trapezoidna.

Definicija. Trokutasta piramida (tetraedar) je piramida u kojoj su tri lica i baza proizvoljni trokuti.

Tetraedar ima četiri lica i četiri vrha i šest bridova, pri čemu bilo koja dva brida nemaju zajedničke vrhove, ali se ne dodiruju.

Svaki vrh se sastoji od tri lica i bridova koji se tvore trokutasti kut.

Segment koji povezuje vrh tetraedra sa središtem suprotne strane naziva se medijan tetraedra(GM).

Bimedijan naziva segment koji spaja središta suprotnih rubova koji se ne dodiruju (KL).

Svi bimedijani i medijani tetraedra sijeku se u jednoj točki (S). U ovom slučaju bimedijane se dijele na pola, a medijane se dijele u omjeru 3:1 počevši od vrha.

Definicija. Kosa piramida je piramida kojoj jedan od bridova s ​​bazom tvori tupi kut (β).

Definicija. Pravokutna piramida je piramida u kojoj je jedna od bočnih strana okomita na bazu.

Definicija. Oštrokutna piramida- piramida u kojoj je apotem duži od polovice stranice baze.

Definicija. Tupa piramida- piramida u kojoj je apotem manji od polovice duljine stranice baze.

Definicija. Pravilni tetraedar- tetraedar u kojem su sva četiri lica jednakostranični trokuti. To je jedan od pet pravilnih poligona. U pravilnom tetraedru svi diedarski kutovi (između ploha) i trokutni kutovi (u vrhu) su jednaki.

Definicija. Pravokutni tetraedar naziva se tetraedar u kojem između tri brida na vrhu (brdovi su okomiti) ima pravi kut. Formiraju se tri lica rectangular trokutasti kut a plohe su pravokutni trokuti, a baza je proizvoljan trokut. Apotem bilo kojeg lica jednak je polovici stranice baze na koju apotem pada.

Definicija. Izoedarski tetraedar naziva se tetraedar čije su bočne strane međusobno jednake, a baza je pravilan trokut. Takav tetraedar ima lica koja su jednakokračni trokuti.

Definicija. Ortocentrični tetraedar zove se tetraedar u kojem se sve visine (okomice) koje su s vrha spuštene na suprotnu plohu sijeku u jednoj točki.

Definicija. Zvjezdana piramida zove se poliedar čija je baza zvijezda.

Definicija. Bipiramida- poliedar koji se sastoji od dvije različite piramide (piramide mogu biti i odrezane), imaju zajedničku bazu, a vrhovi leže na suprotnim stranama ravnine baze.

Prilikom pripreme za jedinstveni državni ispit iz matematike, učenici moraju sistematizirati svoje znanje iz algebre i geometrije. Želio bih kombinirati sve poznate informacije, na primjer, o tome kako izračunati površinu piramide. Štoviše, počevši od baze i bočnih rubova do cijele površine. Ako je situacija s bočnim stranama jasna, budući da su trokuti, tada je baza uvijek drugačija.

Kako pronaći područje baze piramide?

To može biti apsolutno bilo koja figura: od proizvoljnog trokuta do n-kuta. A ta baza, osim razlike u broju kutova, može biti pravilan lik ili nepravilan. U zadacima Jedinstvenog državnog ispita koji zanimaju školarce postoje samo zadaci s točnim brojkama u osnovi. Stoga ćemo govoriti samo o njima.

Pravilni trokut

Odnosno, jednakostraničan. Ona u kojoj su sve strane jednake i označene slovom "a". U ovom slučaju, površina baze piramide izračunava se formulom:

S = (a 2 * √3) / 4.

Kvadrat

Formula za izračunavanje njegove površine je najjednostavnija, ovdje je "a" opet strana:

Proizvoljni pravilni n-kut

Stranica poligona ima istu oznaku. Za broj kutova koristi se latinično slovo n.

S = (n * a 2) / (4 * tg (180º/n)).

Što učiniti pri izračunu bočne i ukupne površine?

Budući da je baza pravilan lik, sva lica piramide su jednaka. Štoviše, svaki od njih je jednakokračan trokut, jer su bočni rubovi jednaki. Zatim, da biste izračunali bočnu površinu piramide, trebat će vam formula koja se sastoji od zbroja identičnih monoma. Broj članova određen je brojem stranica baze.

Površina jednakokračnog trokuta izračunava se formulom u kojoj se polovica umnoška baze množi s visinom. Ova visina u piramidi naziva se apotemom. Njegova oznaka je "A". Opća formula za bočnu površinu je:

S = ½ P*A, gdje je P opseg baze piramide.

Postoje situacije kada stranice baze nisu poznate, ali su zadani bočni bridovi (c) i ravni kut pri njezinu vrhu (α). Zatim morate koristiti sljedeću formulu za izračunavanje bočne površine piramide:

S = n/2 * u 2 sin α .

Zadatak br. 1

Stanje. Nađite ukupnu površinu piramide ako njezina baza ima stranicu 4 cm, a apotem ima vrijednost √3 cm.

Riješenje. Morate početi izračunavanjem perimetra baze. Budući da je ovo pravilan trokut, tada je P = 3 * 4 = 12 cm. Budući da je apotem poznat, možemo odmah izračunati površinu cijele bočne površine: ½ * 12 * √3 = 6√3 cm 2.

Za trokut u osnovi dobivate sljedeću vrijednost površine: (4 2 *√3) / 4 = 4√3 cm 2.

Da biste odredili cijelu površinu, morat ćete zbrojiti dvije dobivene vrijednosti: 6√3 + 4√3 = 10√3 cm 2.

Odgovor. 10√3 cm 2.

Problem br. 2

Stanje. Postoji pravilna četverokutna piramida. Duljina donje stranice je 7 mm, bočnog ruba 16 mm. Potrebno je saznati njegovu površinu.

Riješenje. Budući da je poliedar četverokutan i pravilan, baza mu je kvadrat. Nakon što saznate površinu baze i bočnih stranica, moći ćete izračunati površinu piramide. Formula za kvadrat je data gore. A za bočne strane poznate su sve strane trokuta. Stoga možete koristiti Heronovu formulu za izračunavanje njihovih površina.

Prvi izračuni su jednostavni i dovode do sljedećeg broja: 49 mm 2. Za drugu vrijednost morat ćete izračunati poluopseg: (7 + 16*2): 2 = 19,5 mm. Sada možete izračunati površinu jednakokračnog trokuta: √(19,5*(19,5-7)*(19,5-16) 2) = √2985,9375 = 54,644 mm 2. Postoje samo četiri takva trokuta, pa ćete ga pri izračunavanju konačnog broja morati pomnožiti s 4.

Ispada: 49 + 4 * 54,644 = 267,576 mm 2.

Odgovor. Željena vrijednost je 267,576 mm 2.

Problem br. 3

Stanje. Za pravilnu četverokutnu piramidu morate izračunati površinu. Poznato je da je stranica kvadrata 6 cm, a visina 4 cm.

Riješenje. Najlakši način je upotrijebiti formulu s umnoškom opsega i apoteme. Prvu vrijednost je lako pronaći. Drugi je malo kompliciraniji.

Morat ćemo se sjetiti Pitagorinog poučka i uzeti u obzir da se sastoji od visine piramide i apoteme, što je hipotenuza. Drugi krak je jednak polovici stranice kvadrata, budući da visina poliedra pada u njegovu sredinu.

Traženi apotem (hipotenuza pravokutnog trokuta) jednak je √(3 2 + 4 2) = 5 (cm).

Sada možete izračunati traženu vrijednost: ½*(4*6)*5+6 2 = 96 (cm 2).

Odgovor. 96 cm 2.

Problem broj 4

Stanje. Dana je točna stranica. Stranice njegove baze su 22 mm, bočni rubovi su 61 mm. Kolika je bočna površina ovog poliedra?

Riješenje. Obrazloženje u njemu je isto kao ono opisano u zadatku br. 2. Samo tamo je dana piramida s kvadratom u bazi, a sada je šesterokut.

Prije svega, osnovna površina izračunava se pomoću gornje formule: (6*22 2) / (4*tg (180º/6)) = 726/(tg30º) = 726√3 cm 2.

Sada morate saznati poluopseg jednakokračnog trokuta, koji je bočna strana. (22+61*2):2 = 72 cm.Preostaje samo pomoću Heronove formule izračunati površinu svakog takvog trokuta, a zatim ga pomnožiti sa šest i dodati onom dobivenom za bazu.

Izračuni pomoću Heronove formule: √(72*(72-22)*(72-61) 2)=√435600=660 cm 2. Izračuni koji će dati bočnu površinu: 660 * 6 = 3960 cm 2. Ostaje ih zbrojiti kako bismo saznali cijelu površinu: 5217,47≈5217 cm 2.

Odgovor. Baza je 726√3 cm2, bočna ploha 3960 cm2, cjelokupni oplošje 5217 cm2.