Kaip rasti taisyklingos piramidės pagrindo plotą. Keturkampės piramidės plotas

Piramidės paviršiaus plotas. Šiame straipsnyje apžvelgsime įprastų piramidžių problemas. Priminsiu, kad taisyklinga piramidė yra piramidė, kurios pagrindas yra taisyklingas daugiakampis, piramidės viršūnė projektuojama į šio daugiakampio centrą.

Tokios piramidės šoninis paviršius yra lygiašonis trikampis.Šio trikampio aukštis, nubrėžtas iš taisyklingos piramidės viršūnės, vadinamas apotema, SF - apotema:

Žemiau pateikto tipo problemos atveju turite rasti visos piramidės paviršiaus plotą arba jos šoninio paviršiaus plotą. Tinklaraštyje jau buvo aptartos kelios įprastų piramidžių problemos, kur klausimas buvo apie elementų (aukštis, pagrindo kraštas, šoninis kraštas) suradimą.

Vieningo valstybinio egzamino užduotyse dažniausiai nagrinėjamos taisyklingos trikampės, keturkampės ir šešiakampės piramidės. Nemačiau jokių problemų dėl įprastų penkiakampių ir septyniakampių piramidžių.

Viso paviršiaus ploto formulė yra paprasta - reikia rasti piramidės pagrindo ploto ir jos šoninio paviršiaus ploto sumą:

Apsvarstykime užduotis:

Taisyklingos keturkampės piramidės pagrindo kraštinės yra 72, šoninės briaunos yra 164. Raskite šios piramidės paviršiaus plotą.

Piramidės paviršiaus plotas lygus šoninio paviršiaus ir pagrindo plotų sumai:

*Šoninis paviršius susideda iš keturių vienodo ploto trikampių. Piramidės pagrindas yra kvadratas.

Piramidės kraštinės plotą galime apskaičiuoti naudodami:

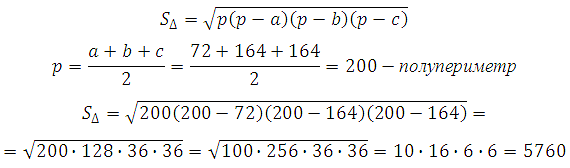
Taigi piramidės paviršiaus plotas yra:

Atsakymas: 28224

Taisyklingos šešiakampės piramidės pagrindo kraštinės lygios 22, šoninės briaunos lygios 61. Raskite šios piramidės šoninio paviršiaus plotą.

Taisyklingos šešiakampės piramidės pagrindas yra taisyklingas šešiakampis.

Šios piramidės šoninį paviršiaus plotą sudaro šeši lygių trikampių plotai, kurių kraštinės yra 61, 61 ir 22:

Raskime trikampio plotą naudodami Herono formulę:

Taigi šoninio paviršiaus plotas yra:

Atsakymas: 3240

*Aukščiau pateiktose problemose šoninio paviršiaus plotą galima rasti naudojant kitą trikampio formulę, tačiau tam reikia apskaičiuoti apotemą.

27155. Raskite taisyklingos keturkampės piramidės, kurios pagrindo kraštinės yra 6, o aukštis 4, paviršiaus plotą.

Norėdami rasti piramidės paviršiaus plotą, turime žinoti pagrindo plotą ir šoninio paviršiaus plotą:

Pagrindo plotas yra 36, nes tai yra kvadratas su 6 kraštine.

Šoninis paviršius susideda iš keturių paviršių, kurie yra lygūs trikampiai. Norėdami rasti tokio trikampio plotą, turite žinoti jo pagrindą ir aukštį (apotemą):

*Trikampio plotas lygus pusei pagrindo sandaugos ir aukščio, nubrėžto iki šio pagrindo.

Pagrindas žinomas, lygus šešiems. Raskime aukštį. Apsvarstykite stačiakampį trikampį (paryškintą geltonai):

Viena koja yra lygi 4, nes tai yra piramidės aukštis, kita lygi 3, nes ji yra lygi pusei pagrindo krašto. Hipotenuzę galime rasti naudodami Pitagoro teoremą:

Tai reiškia, kad piramidės šoninio paviršiaus plotas yra:

Taigi visos piramidės paviršiaus plotas yra:

Atsakymas: 96

27069. Taisyklingos keturkampės piramidės pagrindo kraštinės lygios 10, šoninės briaunos lygios 13. Raskite šios piramidės paviršiaus plotą.

27070. Taisyklingos šešiakampės piramidės pagrindo kraštinės lygios 10, šoninės briaunos lygios 13. Raskite šios piramidės šoninio paviršiaus plotą.

Taip pat yra įprastos piramidės šoninio paviršiaus ploto formulės. Įprastoje piramidėje pagrindas yra stačiakampė šoninio paviršiaus projekcija, todėl:

P- bazinis perimetras, l- piramidės apotema

*Ši formulė pagrįsta trikampio ploto formule.

Jei norite sužinoti daugiau apie tai, kaip gaunamos šios formulės, nepraleiskite to, sekite straipsnių publikaciją.Tai viskas. Sėkmės tau!

Pagarbiai Aleksandras Krutitskichas.

P.S. Būčiau dėkingas, jei papasakotumėte apie svetainę socialiniuose tinkluose.

Prieš tyrinėdami klausimus apie šią geometrinę figūrą ir jos savybes, turėtumėte suprasti kai kuriuos terminus. Išgirdęs apie piramidę žmogus įsivaizduoja didžiulius pastatus Egipte. Taip atrodo patys paprasčiausi. Tačiau jie būna įvairių tipų ir formų, o tai reiškia, kad geometrinių formų skaičiavimo formulė skirsis.

Piramidė – geometrinė figūra, žymintys ir atstovaujantys kelis veidus. Iš esmės tai yra tas pats daugiakampis, kurio pagrindu yra daugiakampis, o šonuose yra trikampiai, kurie jungiasi viename taške - viršūnėje. Figūra būna dviejų pagrindinių tipų:

teisingas;
sutrumpintas.

Pirmuoju atveju pagrindas yra taisyklingas daugiakampis. Čia visi šoniniai paviršiai yra lygūs tarp savęs ir pačios figūros patiks perfekcionisto akį.

Antruoju atveju yra du pagrindai – didelis pačiame apačioje ir mažas tarp viršaus, kartojantis pagrindinio formą. Kitaip tariant, nupjauta piramidė yra daugiakampis, kurio skerspjūvis suformuotas lygiagrečiai pagrindui.

Terminai ir simboliai

Pagrindiniai terminai:

Taisyklingas (lygiakrais) trikampis- figūra su trimis vienodais kampais ir lygiomis kraštinėmis. Šiuo atveju visi kampai yra 60 laipsnių. Figūra yra paprasčiausia iš įprastų daugiakampių. Jei šis skaičius yra prie pagrindo, toks daugiakampis bus vadinamas taisyklingu trikampiu. Jei pagrindas yra kvadratas, piramidė bus vadinama taisyklinga keturkampe piramide.
Viršūnė– aukščiausias taškas, kur susikerta kraštai. Viršūnės aukštį sudaro tiesi linija, besitęsianti nuo viršūnės iki piramidės pagrindo.
Kraštas– viena iš daugiakampio plokštumų. Trikampės piramidės atveju jis gali būti trikampio formos arba nupjautos piramidės trapecijos formos.
Skyrius- plokščia figūra, susidariusi dėl skrodimo. Jo nereikėtų painioti su skyriumi, nes sekcija taip pat parodo, kas yra už skyriaus.
Apotema- segmentas, nubrėžtas nuo piramidės viršaus iki jos pagrindo. Tai taip pat yra veido aukštis, kuriame yra antrasis aukščio taškas. Šis apibrėžimas galioja tik taisyklingo daugiakampio atžvilgiu. Pavyzdžiui, jei tai nėra nupjauta piramidė, veidas bus trikampis. Šiuo atveju šio trikampio aukštis taps apotema.

Ploto formulės

Raskite piramidės šoninio paviršiaus plotą bet kokio tipo galima atlikti keliais būdais. Jei figūra nėra simetriška ir yra daugiakampis su skirtingomis kraštinėmis, tokiu atveju lengviau apskaičiuoti bendrą paviršiaus plotą per visų paviršių visumą. Kitaip tariant, turite apskaičiuoti kiekvieno veido plotą ir pridėti juos kartu.

Atsižvelgiant į tai, kokie parametrai yra žinomi, gali prireikti kvadrato, trapecijos, savavališko keturkampio ir kt. Pačios formulės skirtingais atvejais taip pat turės skirtumų.

Įprastos figūros atveju plotą rasti daug lengviau. Pakanka žinoti tik kelis pagrindinius parametrus. Daugeliu atvejų skaičiavimai reikalingi būtent tokiems skaičiams. Todėl atitinkamos formulės bus pateiktos žemiau. Priešingu atveju tektų viską surašyti per kelis puslapius, o tai tik suklaidintų ir suklaidintų.

Pagrindinė skaičiavimo formulė Taisyklingos piramidės šoninio paviršiaus plotas bus toks:

S = ½ Pa (P yra pagrindo perimetras ir apotemas)

Pažvelkime į vieną pavyzdį. Daugiakampis turi pagrindą su atkarpomis A1,A2,A3,A4,A5,ir visi jie lygūs 10cm.Tegul apotemas lygus 5cm.Pirmiausia reikia rasti perimetrą. Kadangi visi penki pagrindo paviršiai yra vienodi, galite jį rasti taip: P = 5 * 10 = 50 cm Toliau taikome pagrindinę formulę: S = ½ * 50 * 5 = 125 cm kvadratu.

Taisyklingos trikampės piramidės šoninis paviršiaus plotas lengviausia apskaičiuoti. Formulė atrodo taip:

S =½* ab *3, kur a yra apotemas, b yra pagrindo paviršius. Trijų koeficientas čia reiškia pagrindo veidų skaičių, o pirmoji dalis yra šoninio paviršiaus plotas. Pažiūrėkime į pavyzdį. Duota figūra, kurios apotemas 5 cm ir pagrindo briauna 8 cm Skaičiuojame: S = 1/2*5*8*3=60 cm kvadratu.

Nupjautos piramidės šoninis paviršiaus plotas Tai šiek tiek sunkiau apskaičiuoti. Formulė atrodo taip: S =1/2*(p_01+ p_02)*a, kur p_01 ir p_02 yra bazių perimetrai ir yra apotemas. Pažiūrėkime į pavyzdį. Tarkime, kad keturkampei figūrai pagrindų kraštinių matmenys yra 3 ir 6 cm, o apotemos - 4 cm.

Čia pirmiausia reikia rasti pagrindų perimetrus: р_01 =3*4=12 cm; р_02=6*4=24 cm Belieka reikšmes pakeisti į pagrindinę formulę ir gauname: S =1/2*(12+24)*4=0,5*36*4=72 cm kvadratu.

Taigi galite rasti bet kokio sudėtingumo taisyklingos piramidės šoninį paviršiaus plotą. Turėtumėte būti atsargūs ir nesupainiotišiuos skaičiavimus su visu daugiakampio plotu. Ir jei jums vis tiek reikia tai padaryti, tiesiog apskaičiuokite didžiausio daugiakampio pagrindo plotą ir pridėkite jį prie daugiakampio šoninio paviršiaus ploto.

Vaizdo įrašas

Šis vaizdo įrašas padės jums konsoliduoti informaciją apie tai, kaip rasti skirtingų piramidžių šoninio paviršiaus plotą.

Negavai atsakymo į savo klausimą? Siūlykite temą autoriams.

Tipinės geometrinės problemos plokštumoje ir trimatėje erdvėje yra skirtingų figūrų paviršiaus plotų nustatymo problemos. Šiame straipsnyje pateikiame taisyklingos keturkampės piramidės šoninio paviršiaus ploto formulę.

Kas yra piramidė?

Pateiksime griežtą geometrinį piramidės apibrėžimą. Tarkime, kad turime daugiakampį su n kraštinių ir n kampų. Pasirinkime savavališką erdvės tašką, kuris nebus nurodyto n kampo plokštumoje, ir sujungsime jį su kiekviena daugiakampio viršūne. Gausime tam tikro tūrio figūrą, kuri vadinama n kampine piramide. Pavyzdžiui, žemiau esančiame paveikslėlyje parodykime, kaip atrodo penkiakampė piramidė.

Du svarbūs bet kurios piramidės elementai yra jos pagrindas (n-kampis) ir viršūnė. Šie elementai yra sujungti vienas su kitu n trikampių, kurie apskritai nėra lygūs vienas kitam. Statmenas, besileidžiantis iš viršaus į pagrindą, vadinamas figūros aukščiu. Jeigu ji kerta pagrindą geometriniame centre (sutampa su daugiakampio masės centru), tai tokia piramidė vadinama tiesia linija. Jei, be šios sąlygos, pagrindas yra taisyklingas daugiakampis, tai visa piramidė vadinama taisyklingąja. Žemiau esančiame paveikslėlyje parodyta, kaip atrodo įprastos piramidės su trikampiais, keturkampiais, penkiakampiais ir šešiakampiais pagrindais.

Piramidės paviršius

Prieš pereidami prie taisyklingos keturkampės piramidės šoninio paviršiaus ploto klausimo, turėtume išsamiau pasidomėti paties paviršiaus samprata.

Kaip minėta aukščiau ir parodyta paveiksluose, bet kurią piramidę sudaro veidų arba šonų rinkinys. Viena kraštinė yra pagrindas, o n kraštinių yra trikampiai. Visos figūros paviršius yra kiekvienos jos kraštinės plotų suma.

Patogu tyrinėti paviršių naudojant figūros raidos pavyzdį. Taisyklingos keturkampės piramidės raida parodyta toliau pateiktuose paveikslėliuose.

Matome, kad jo paviršiaus plotas yra lygus keturių vienodų lygiašonių trikampių plotų ir kvadrato ploto sumai.

Bendras visų trikampių, sudarančių figūros kraštines, plotas paprastai vadinamas šoniniu paviršiaus plotu. Toliau parodysime, kaip jį apskaičiuoti taisyklingai keturkampei piramidei.

Keturkampės taisyklingos piramidės šoninis paviršiaus plotas

Norėdami apskaičiuoti nurodytos figūros šoninį paviršiaus plotą, vėl kreipiamės į aukščiau pateiktą raidą. Tarkime, kad žinome kvadratinio pagrindo pusę. Pažymėkime jį simboliu a. Matyti, kad kiekvienas iš keturių vienodų trikampių turi pagrindą, kurio ilgis yra a. Norėdami apskaičiuoti jų bendrą plotą, turite žinoti šią vieno trikampio vertę. Iš geometrijos kurso žinome, kad trikampio plotas S t lygus pagrindo ir aukščio sandaugai, kurią reikia padalyti per pusę. Tai yra:

Kur h b yra lygiašonio trikampio, nubrėžto iki pagrindo a, aukštis. Piramidei šis aukštis yra apotema. Dabar belieka gautą išraišką padauginti iš 4, kad gautumėte nagrinėjamos piramidės šoninio paviršiaus plotą S b:

S b = 4*S t = 2*h b *a.

Šioje formulėje yra du parametrai: apotemas ir pagrindo pusė. Jei pastarasis yra žinomas daugeliu probleminių sąlygų, tai pirmasis turi būti skaičiuojamas žinant kitus dydžius. Štai formulės, skirtos apotemos h b apskaičiavimui dviem atvejais:

kai žinomas šoninio šonkaulio ilgis;
kai žinomas piramidės aukštis.

Jei šoninės briaunos (lygiašonio trikampio kraštinės) ilgį žymėsime simboliu L, tai apotema h b nustatoma pagal formulę:

h b = √(L 2 - a 2 /4).

Ši išraiška yra Pitagoro teoremos taikymo šoniniam paviršiaus trikampiui rezultatas.

Jei žinomas piramidės aukštis h, tada apotemą h b galima apskaičiuoti taip:

h b = √(h 2 + a 2 /4).
Taip pat nesunku gauti šią išraišką, jei nagrinėsime piramidės viduje esantį statųjį trikampį, sudarytą iš kojų h ir a/2 bei hipotenuzos h b.
Parodykime, kaip pritaikyti šias formules, išspręsdami dvi įdomias problemas.

Problema su žinomu paviršiaus plotu

Yra žinoma, kad keturkampio šoninio paviršiaus plotas yra 108 cm 2. Būtina apskaičiuoti jo apotemos ilgį h b, jei piramidės aukštis yra 7 cm.
Parašykime šoninio paviršiaus ploto S b formulę aukščiu. Mes turime:

S b = 2*√(h 2 + a 2 /4) *a.

Čia mes tiesiog pakeitėme atitinkamą apotemos formulę į S b išraišką. Padėkime abi lygties puses kvadratu:

S b 2 = 4 * a 2 * h 2 + a 4.

Norėdami rasti a reikšmę, pakeičiame kintamuosius:

t 2 + 4*h 2 *t - S b 2 = 0.

Dabar pakeičiame žinomas reikšmes ir išsprendžiame kvadratinę lygtį:

t 2 + 196*t - 11664 = 0.

Užrašėme tik teigiamą šios lygties šaknį. Tada piramidės pagrindo kraštinės bus lygios:

a = √t = √47,8355 ≈ 6,916 cm.

Norėdami gauti apotemos ilgį, tiesiog naudokite formulę:

h b = √(h 2 + a 2 /4) = √(7 2 + 6,916 2 /4) ≈ 7,808 cm.

Cheopso piramidės šoninis paviršius

Nustatykime didžiausios Egipto piramidės šoninio paviršiaus ploto vertę. Yra žinoma, kad jo bazėje yra kvadratas, kurio kraštinės ilgis yra 230 363 metrai. Iš pradžių statinio aukštis buvo 146,5 metro. Pakeiskite šiuos skaičius į atitinkamą S b formulę, gausime:

S b = 2*√(h 2 + a 2 /4) *a = 2*√(146,5 2 +230,363 2 /4)* 230,363 ≈ 85 860 m 2.

Rasta vertė yra šiek tiek didesnė už 17 futbolo aikščių plotą.

Apibrėžimas. Šoninis kraštas- tai trikampis, kurio vienas kampas yra piramidės viršuje, o priešinga pusė sutampa su pagrindo (daugiakampio) kraštine.

Apibrėžimas. Šoniniai šonkauliai- tai yra bendros šoninių paviršių pusės. Piramidė turi tiek briaunų, kiek daugiakampio kampų.

Apibrėžimas. Piramidės aukštis- tai statmenas, nuleistas nuo piramidės viršaus iki pagrindo.

Apibrėžimas. Apotema- tai statmenas piramidės šoniniam paviršiui, nuleistas nuo piramidės viršaus į pagrindo šoną.

Apibrėžimas. Įstrižainė pjūvis- tai piramidės atkarpa plokštuma, einanti per piramidės viršūnę ir pagrindo įstrižainę.

Apibrėžimas. Teisinga piramidė yra piramidė, kurios pagrindas yra taisyklingas daugiakampis, o aukštis nusileidžia į pagrindo centrą.

Piramidės tūris ir paviršiaus plotas

Formulė. Piramidės tūris per pagrindo plotą ir aukštį:

Piramidės savybės

Jei visos šoninės briaunos lygios, tai aplink piramidės pagrindą galima nubrėžti apskritimą, o pagrindo centras sutampa su apskritimo centru. Taip pat iš viršaus nuleistas statmuo eina per pagrindo (apskritimo) centrą.

Jei visi šoniniai kraštai yra vienodi, tada jie yra pasvirę į pagrindo plokštumą tais pačiais kampais.

Šoninės briaunos yra lygios, kai sudaro vienodus kampus su pagrindo plokštuma arba jei aplink piramidės pagrindą galima apibūdinti apskritimą.

Jei šoniniai paviršiai yra pasvirę į pagrindo plokštumą tuo pačiu kampu, tada į piramidės pagrindą galima įrašyti apskritimą, o piramidės viršūnė projektuojama jo centre.

Jei šoniniai paviršiai yra pasvirę į pagrindo plokštumą tuo pačiu kampu, tada šoninių paviršių apotemos yra lygios.

Taisyklingos piramidės savybės

1. Piramidės viršus yra vienodu atstumu nuo visų pagrindo kampų.

2. Visos šoninės briaunos lygios.

3. Visi šoniniai šonkauliai yra pasvirę vienodais kampais į pagrindą.

4. Visų šoninių paviršių apotemos yra lygios.

5. Visų šoninių paviršių plotai lygūs.

6. Visi paviršiai turi vienodus dvikampius (plokščius) kampus.

7. Aplink piramidę galima apibūdinti sferą. Apribotos sferos centras bus statmenų, einančių per kraštinių vidurį, susikirtimo taškas.

8. Į piramidę galite sutalpinti rutulį. Įbrėžtos sferos centras bus iš kampo tarp briaunos ir pagrindo kylančių bisektorių susikirtimo taškas.

9. Jei įbrėžto rutulio centras sutampa su apriboto rutulio centru, tai plokštumos kampų suma viršūnėje yra lygi π arba atvirkščiai, vienas kampas lygus π/n, kur n yra skaičius kampų piramidės pagrinde.

Piramidės ir sferos ryšys

Aplink piramidę galima apibūdinti sferą, kai piramidės pagrinde yra daugiakampis, aplink kurį galima apibūdinti apskritimą (būtina ir pakankama sąlyga). Rutulio centras bus plokštumų, einančių statmenai per piramidės šoninių kraštų vidurio taškus, susikirtimo taškas.

Visada galima apibūdinti sferą aplink bet kurią trikampę ar taisyklingą piramidę.

Į piramidę galima įrašyti sferą, jei piramidės vidinių dvikampių kampų bisektorinės plokštumos susikerta viename taške (būtina ir pakankama sąlyga). Šis taškas bus sferos centras.

Piramidės sujungimas su kūgiu

Sakoma, kad kūgis yra įrašytas į piramidę, jei jų viršūnės sutampa, o kūgio pagrindas yra įrašytas į piramidės pagrindą.

Į piramidę galima įrašyti kūgį, jei piramidės apotemai yra lygūs vienas kitam.

Sakoma, kad kūgis yra apibrėžiamas aplink piramidę, jei jų viršūnės sutampa, o kūgio pagrindas yra aplink piramidės pagrindą.

Aplink piramidę galima apibūdinti kūgį, jei visos piramidės šoninės briaunos yra lygios viena kitai.

Piramidės ir cilindro ryšys

Piramidė vadinama įbrėžta į cilindrą, jei piramidės viršūnė yra ant vieno cilindro pagrindo, o piramidės pagrindas yra įbrėžtas kitame cilindro pagrinde.

Cilindras gali būti apibūdintas aplink piramidę, jei aplink piramidės pagrindą galima apibūdinti apskritimą.

Apibrėžimas. Nupjauta piramidė (piramidinė prizmė) yra daugiakampis, esantis tarp piramidės pagrindo ir pjūvio plokštumos, lygiagrečios pagrindui. Taigi piramidė turi didesnį pagrindą ir mažesnį pagrindą, panašų į didesnį. Šoniniai paviršiai yra trapecijos formos.

Apibrėžimas. Trikampė piramidė (tetraedras) yra piramidė, kurios trys paviršiai ir pagrindas yra savavališki trikampiai.

Tetraedras turi keturis paviršius ir keturias viršūnes bei šešias briaunas, kur bet kurios dvi briaunos neturi bendrų viršūnių, bet nesiliečia.

Kiekviena viršūnė susideda iš trijų formuojančių paviršių ir briaunų trikampio kampo.

Atkarpa, jungianti tetraedro viršūnę su priešingo paviršiaus centru, vadinama tetraedro mediana(GM).

Bimedian vadinama atkarpa, jungiančia priešingų kraštinių, kurie nesiliečia, vidurio taškus (KL).

Visos tetraedro bimedianos ir medianos susikerta viename taške (S). Šiuo atveju bimedianos dalijamos per pusę, o medianos – santykiu 3:1, pradedant nuo viršaus.

Apibrėžimas. Pasvirusi piramidė yra piramidė, kurios viena iš kraštinių sudaro bukąjį kampą (β) su pagrindu.

Apibrėžimas. Stačiakampė piramidė yra piramidė, kurios vienas iš šoninių paviršių yra statmenas pagrindui.

Apibrėžimas. Ūmaus kampo piramidė- piramidė, kurioje apotemas yra daugiau nei pusė pagrindo kraštinės ilgio.

Apibrėžimas. Bukoji piramidė- piramidė, kurioje apotemas yra mažesnis nei pusė pagrindo kraštinės ilgio.

Apibrėžimas. Taisyklingas tetraedras- tetraedras, kurio visi keturi paviršiai yra lygiakraščiai trikampiai. Tai vienas iš penkių taisyklingų daugiakampių. Įprastame tetraedre visi dvikampiai kampai (tarp paviršių) ir trikampiai kampai (viršūnėje) yra lygūs.

Apibrėžimas. Stačiakampis tetraedras vadinamas tetraedru, kurio viršūnėje tarp trijų kraštinių yra stačiakampis (kraštinės statmenos). Susidaro trys veidai stačiakampis trikampis kampas ir paviršiai yra stačiakampiai, o pagrindas yra savavališkas trikampis. Bet kurio veido apotemas yra lygus pusei pagrindo, ant kurio krenta apotema, kraštinės.

Apibrėžimas. Izoedrinis tetraedras vadinamas tetraedru, kurio šoniniai paviršiai yra lygūs vienas kitam, o pagrindas yra taisyklingasis trikampis. Toks tetraedras turi lygiašonius trikampius.

Apibrėžimas. Ortocentrinis tetraedras vadinamas tetraedru, kuriame visi aukščiai (statmenys), nuleisti iš viršaus į priešingą paviršių, susikerta viename taške.

Apibrėžimas. Žvaigždžių piramidė vadinamas daugiakampiu, kurio pagrindas yra žvaigždė.

Apibrėžimas. Bipiramidė- daugiakampis, susidedantis iš dviejų skirtingų piramidžių (piramidės taip pat gali būti nupjautos), turinčios bendrą pagrindą, o viršūnės yra priešingose pagrindo plokštumos pusėse.

Ruošdamiesi vieningam valstybiniam matematikos egzaminui, studentai turi susisteminti algebros ir geometrijos žinias. Norėčiau sujungti visą žinomą informaciją, pavyzdžiui, kaip apskaičiuoti piramidės plotą. Be to, pradedant nuo pagrindo ir šoninių kraštų iki viso paviršiaus ploto. Jei padėtis su šoniniais paviršiais yra aiški, nes jie yra trikampiai, tada pagrindas visada skiriasi.

Kaip rasti piramidės pagrindo plotą?

Tai gali būti visiškai bet kokia figūra: nuo savavališko trikampio iki n kampo. Ir ši bazė, be kampų skaičiaus skirtumo, gali būti taisyklinga figūra arba netaisyklinga. Vieningo valstybinio egzamino užduotyse, kurios domina moksleivius, yra tik užduotys su teisingomis skaičiais. Todėl kalbėsime tik apie juos.

Taisyklingas trikampis

Tai yra lygiakraštis. Tas, kurio visos pusės yra lygios ir pažymėtos raide „a“. Šiuo atveju piramidės pagrindo plotas apskaičiuojamas pagal formulę:

S = (a 2 * √3) / 4.

Kvadratas

Jo ploto apskaičiavimo formulė yra pati paprasčiausia, čia „a“ vėl yra pusė:

Savavališkas reguliarus n-gonas

Daugiakampio kraštinė turi tą patį žymėjimą. Kampų skaičiui nurodoma lotyniška raidė n.

S = (n * a 2) / (4 * tg (180º/n)).

Ką daryti skaičiuojant šoninį ir bendrą paviršiaus plotą?

Kadangi pagrindas yra taisyklinga figūra, visi piramidės paviršiai yra vienodi. Be to, kiekvienas iš jų yra lygiašonis trikampis, nes šoninės briaunos yra lygios. Tada, norint apskaičiuoti piramidės šoninį plotą, jums reikės formulės, sudarytos iš identiškų monomijų sumos. Terminų skaičius nustatomas pagal pagrindo kraštų skaičių.

Lygiašonio trikampio plotas apskaičiuojamas pagal formulę, kurioje pusė pagrindo sandaugos padauginama iš aukščio. Šis aukštis piramidėje vadinamas apotema. Jo žymėjimas yra „A“. Bendra šoninio paviršiaus ploto formulė yra tokia:

S = ½ P*A, kur P yra piramidės pagrindo perimetras.

Pasitaiko situacijų, kai pagrindo kraštinės nežinomos, bet pateikiamos šoninės briaunos (c) ir plokščiasis kampas jo viršūnėje (α). Tada, norėdami apskaičiuoti piramidės šoninį plotą, turite naudoti šią formulę:

S = n/2 * 2 sin α .

Užduotis Nr.1

Būklė. Raskite bendrą piramidės plotą, jei jos pagrindo kraštinė yra 4 cm, o apotemos reikšmė yra √3 cm.

Sprendimas. Pradėti reikia nuo pagrindo perimetro apskaičiavimo. Kadangi tai yra taisyklingas trikampis, tai P = 3*4 = 12 cm. Kadangi apotema žinoma, galime iš karto apskaičiuoti viso šoninio paviršiaus plotą: ½*12*√3 = 6√3 cm 2.

Trikampiui prie pagrindo gaunama tokia ploto reikšmė: (4 2 *√3) / 4 = 4√3 cm 2.

Norėdami nustatyti visą plotą, turėsite pridėti dvi gautas reikšmes: 6√3 + 4√3 = 10√3 cm 2.

Atsakymas. 10√3 cm 2.

2 problema

Būklė. Yra taisyklinga keturkampė piramidė. Pagrindo kraštinės ilgis 7 mm, šoninis kraštas 16 mm. Būtina išsiaiškinti jo paviršiaus plotą.

Sprendimas. Kadangi daugiakampis yra keturkampis ir taisyklingas, jo pagrindas yra kvadratas. Sužinoję pagrindo ir šoninių paviršių plotą, galėsite apskaičiuoti piramidės plotą. Kvadrato formulė pateikta aukščiau. O šoniniams paviršiams žinomos visos trikampio kraštinės. Todėl jų plotams apskaičiuoti galite naudoti Herono formulę.

Pirmieji skaičiavimai yra paprasti ir leidžia gauti tokį skaičių: 49 mm 2. Dėl antrosios vertės turėsite apskaičiuoti pusiau perimetrą: (7 + 16 * 2): 2 = 19,5 mm. Dabar galite apskaičiuoti lygiašonio trikampio plotą: √(19,5*(19,5-7)*(19,5-16) 2) = √2985,9375 = 54,644 mm 2. Tokių trikampių yra tik keturi, todėl skaičiuojant galutinį skaičių turėsite jį padauginti iš 4.

Pasirodo: 49 + 4 * 54,644 = 267,576 mm 2.

Atsakymas. Norima vertė yra 267,576 mm2.

3 problema

Būklė. Įprastai keturkampei piramidei reikia apskaičiuoti plotą. Žinoma, kad kvadrato kraštinė yra 6 cm, o aukštis - 4 cm.

Sprendimas. Lengviausias būdas yra naudoti formulę su perimetro ir apotemos sandauga. Pirmąją vertę lengva rasti. Antrasis yra šiek tiek sudėtingesnis.

Turėsime prisiminti Pitagoro teoremą ir manyti, kad ją sudaro piramidės aukštis ir apotemas, kuris yra hipotenuzė. Antroji kojelė yra lygi pusei kvadrato kraštinės, nes daugiakampio aukštis patenka į jo vidurį.

Reikalingas apotemas (stačiojo trikampio hipotenūza) lygus √(3 2 + 4 2) = 5 (cm).

Dabar galite apskaičiuoti reikiamą reikšmę: ½*(4*6)*5+6 2 = 96 (cm 2).

Atsakymas. 96 cm2.

Problema Nr.4

Būklė. Nurodyta teisinga kraštinė, jos pagrindo kraštinės 22 mm, šoninės briaunos 61 mm. Koks yra šio daugiakampio šoninio paviršiaus plotas?

Sprendimas. Motyvacija jame yra tokia pati, kaip aprašyta užduotyje Nr. Tik ten buvo duota piramidė su kvadratu prie pagrindo, o dabar ji yra šešiakampė.

Visų pirma, bazinis plotas apskaičiuojamas pagal aukščiau pateiktą formulę: (6*22 2) / (4*tg (180º/6)) = 726/(tg30º) = 726√3 cm 2.

Dabar reikia išsiaiškinti lygiašonio trikampio, kuris yra šoninis paviršius, pusiau perimetrą. (22+61*2):2 = 72 cm. Belieka pagal Herono formulę apskaičiuoti kiekvieno tokio trikampio plotą, o tada padauginti iš šešių ir pridėti prie gauto pagrindo.

Skaičiavimai pagal Herono formulę: √(72*(72-22)*(72-61) 2)=√435600=660 cm 2. Skaičiavimai, kurie duos šoninio paviršiaus plotą: 660 * 6 = 3960 cm 2. Belieka juos pridėti, kad sužinotumėte visą paviršių: 5217,47≈5217 cm 2.

Atsakymas. Pagrindas 726√3 cm2, šoninis paviršius 3960 cm2, visas plotas 5217 cm2.